Анализ размерностей. Число Рейнольдса.

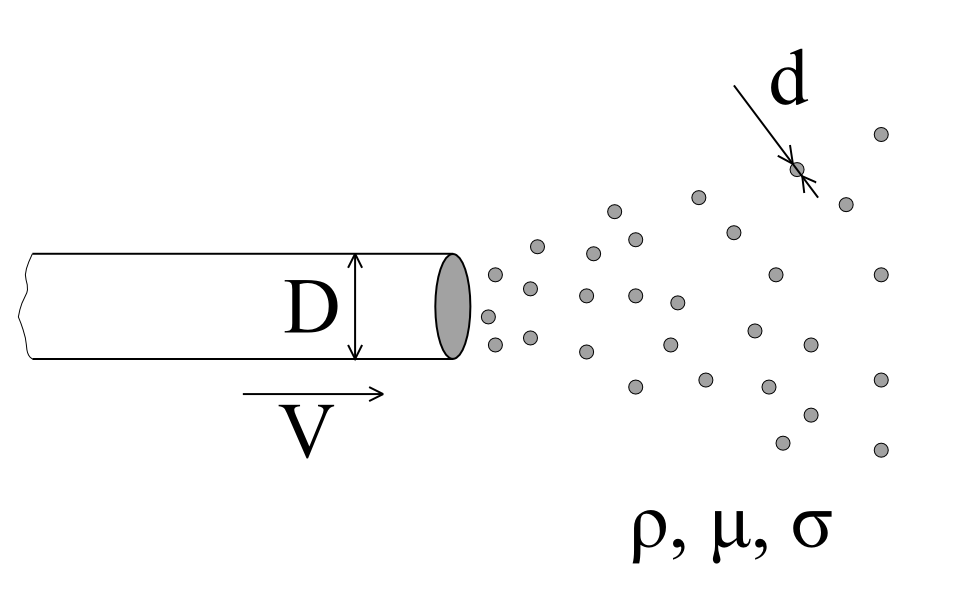
Схема эксперимента. Анализ размерностей — Анализ размерностей — Схема эксперимента. Суть: из трубки, например, форсунки, распыляется жидкость. Задача — составить уравнение того, как зависит диаметр $d$ (зависимая переменная) от остальных (независимых) переменных, показанных на рисунке. $\rho$ — плотность жидкости, $\mu$ — кинематическая вязкость, $\sigma$ — поверхностное натяжение.

Итак, анализ размерностей. Ссылка на видео-урок Гая Рифлера. Урок на английском языке. Интересный факт о числе Рейнольдса. Его можно получить вообще без аэродинамики, а только лишь рассматривая свойства единиц измерения задачи или эксперимента. В данной статье приведу текстовую версию на русском языке.

Анализ размерностей. Общие сведения

Допустим, для показанной на рисунке задачи нет уравнения и нам нужно его построить. В принципе, можно начать масштабную серию экспериментов и рано или поздно прийти к результатам. Но обратите внимание, для пяти независимых переменных, поиск функции вида $d=f(D,V,\rho,\mu,\sigma)$ становится почти неразрешимой задачей. Серия экспериментов будет огромной. Применяемость на практике результатов, достигнутых с большим трудом будет под вопросом.

Анализ размерностей позволяет свести задачу к меньшему числу независимых переменных, называемых Пи-числами (безразмерными переменными). Для получения безразмерных Пи-чисел, используется Пи-теорема Бакингема.

Пару слов о единицах измерения. Все исходные единицы измерения, показанные на рисунке, кроме диаметров, являются производными. В зарубежной литературе по гидродинамике можно встретить два обозначения системы основных единиц измерения:

MLT — «Mass Length Time»
FLT — «Force Length Time»

Например, плотность (производная единица) в системе MLT имеет размерность $M/L^{3}$ . Но $F=ma$ , поэтому масса в системе FLT имеет вид $N/(L/T^{2})=FT^{2}/L$ . А это значит, что плотность в системе FLT имеет размерность $\frac{FT^{2}}{L^{4}}$ .

Единицы MLT и FLT измерения относятся к основным единицам. См. сайт Международного бюро мер и весов. Но их берется три, а не все семь. Потому что некоторые основные единицы в задаче не участвуют. В нашей задаче шесть исходных и три основных единицы измерения.

Единицы измерения переменных

Для нашей задачи, запишем единицы измерения в системе MLT. Равенство с точкой означает «имеет единицы измерения».

Диаметр $d \dot{=}L$
Диаметр $D \dot{=}L$
Скорость $М \dot{=}LT^{-1}$
Плотность $\rho \dot{=}ML^{-3}$
Кинематическая вязкость $\mu \dot{=}ML^{-1}T^{-1}$
Поверхностное натяжение $\sigma \dot{=}MT^{-2}$

Пи-теорема Бакингема

Число независимых безразмерных чисел $\Pi_{i}$ , которые можно получить из анализа размерностей равно $k-r$ , где $k$ — общее число исходных переменных, в том числе и зависимая переменная $d$ , а $r$ — число основных единиц измерения в задаче. В нашем случае, число безразмерных Пи-чисел равно $6-3=3$ шт.

То есть $d=f(D,V,\rho,\mu,\sigma)$ можно привести к $\Pi_{1}=\phi(\Pi_{2},\Pi_{3})$ .

Метод повторяющихся переменных

Как же получить безразмерные переменные и сформулировать задачу в них? Для этого необходимо предпринять два шага:

Шаг 1. Выбрать повторяющиеся переменные,
Шаг 2. Получить безразмерные переменные;

Рассмотрим эти шаги подробнее.

Шаг 1. Выбор повторяющихся переменных

Сначала выберем в количестве $r$ , то есть три штуки, единицы из исходных и поместим их в группу повторяющихся единиц. В эту группу должны войти единицы, формирующие набор со следующими свойствами:

В списке нет зависимых единиц (нельзя сделать так, чтобы манипуляции с исходными единицами привели бы к сокращению всех основных единиц измерения).
В наборе повторяющихся должны быть представлены все $r$ основных единиц измерения.
В повторяющиеся не должна входить сама функция, т.е. $d$ .

Возьмем, к примеру, такой набор повторяющихся переменных:

$\begin{cases} D \dot{=}L \\ \mu \dot{=}ML^{-1}T^{-1} \\ V \dot{=}LT^{-1} \end{cases}$

Это правильный набор. Он соответствует требованиям 1-3 данного шага.

Вот такой набор — тоже правильный:

$\begin{cases} D \dot{=}L \\ \sigma \dot{=}MT^{-2} \\ \rho \dot{=}ML^{-3} \end{cases}$

Следует заметить, что различные повторяющиеся переменные будут приводить к различным безразмерным Пи-числам. Теперь, чтобы не сложилось мнения о том, что любой набор исходных переменных сгодится для группы повторяющихся, приведем такие наборы, которые нельзя выбирать.

$\begin{cases} \sigma \dot{=}MT^{-2} \\ \mu \dot{=}ML^{-1}T^{-1} \\ V \dot{=}LT^{-1} \end{cases}$

Почему нельзя: $(\frac{\sigma}{\mu})/V=1$ . Набор не обладает свойством №1. Еще один пример:

$\begin{cases} d \dot{=}L \\ \sigma \dot{=}MT^{-2} \\ \rho \dot{=}ML^{-3} \end{cases}$

Этот набор не проходит по правилу №3. И ещё один неправильный:

$\begin{cases} d \dot{=}L \\ D \dot{=}L \\ V \dot{=}LT^{-1} \end{cases}$

Данный набор не проходит по правилу №1, т.к. $\frac{d}{D}\dot{=}1$ , и он также не проходит по правилу №2 — представлены только две из трех основных единиц измерения. По правилу №3 тоже не проходит $d$ в этом наборе быть не должно.

Шаг 2. Получим безразмерные переменные (Пи-числа)

Допустим, мы выбрали в качестве повторяющихся переменные $D,\mu,V$ . Остальные тогда ( $d,\rho,\sigma$ ) остаются не повторяющимися. Для каждой не повторяющейся переменной, определяем такие умножения и деления на повторяющиеся (можно со степенями), чтобы получилась единица. Т.е. стараемся сократить все основные единицы измерения.

$\Pi_{1}$ : $d \dot{=}L$ . Тут всё просто. Чтобы получилась единица, надо поделить на $D$ . Поэтому $\mathbf{\Pi_{1}=\frac{d}{D}}$

$\Pi_{2}$ : $\rho \dot{=}ML^{-3}$ Тут посложнее. Сначала поделим $\rho/\mu\dot{=}\frac{ML^{-3}}{ML^{-1}T^{-1}}$ . $M$ сократилась. Затем, нужно ликвидировать $T$ , для чего умножаем результат на $V$ . $\rho V/\mu\dot{=}\frac{L^{-3}LT^{-1}}{L^{-1}T^{-1}}$ . $T$ сократились, остаются L. Используем $D$ . $\rho V D/\mu\dot{=} 1$ .

Мы получили безразмерное число Рейнольдса. $\mathbf{\Pi_{2}=\frac{\rho V D}{\mu}}$ .

$\Pi_{3}$ : $\sigma \dot{=}MT^{-2}$ . Делим на $\mu$ (сократится масса), затем делим на $V$ (сократится $T$ и получится 1). Таким образом, $\mathbf{\Pi_{3}=\frac{\sigma}{\mu V}}$ .

Вывод

Задача отыскания функции в виде $d=f(D,V,\rho,\mu,\sigma)$ сведена к исследованию функции в безразмерных величинах $\Pi_{1}=\phi(\Pi_{2},\Pi_{3})$ .

Wolfram Alpha

Вот как работает с размерностями Wolfram Alpha. См. раздел Dimensionless Combinations.

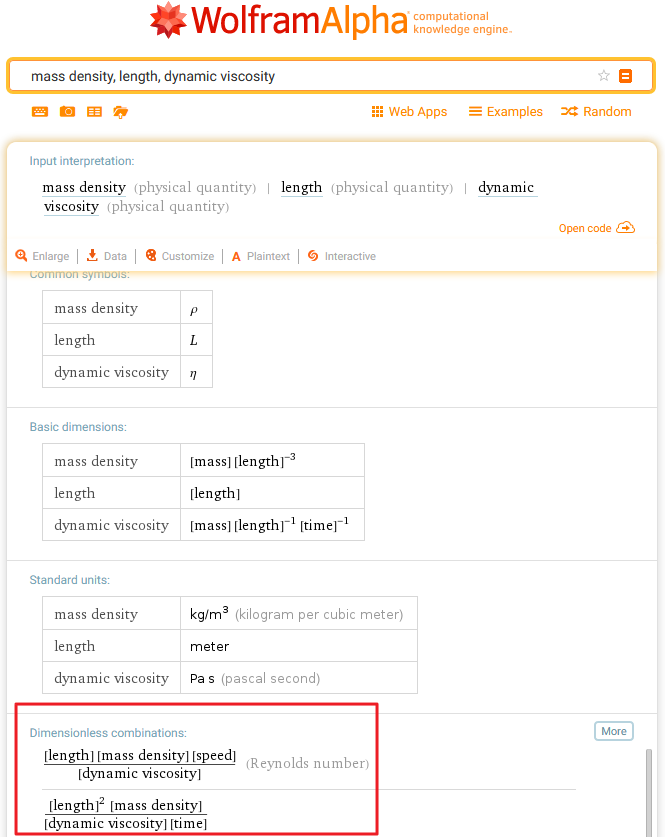
Здесь я пока не понял, как сделать два диаметра, вместо одного Length, чтобы получить $\Pi_{1}=\frac{d}{D}$ .